√abの作図方法
2次方程式の利用〜箱〜
よくある問題です。正方形の紙の四隅を切って,容器を作り,その容積が〇〇のとき,何cm四隅を切り取ったでしょうかという問題です。その「四隅を切り取って容器を作る」がイメージできるために作りました。
2次方程式の利用〜道幅〜
畑の面積を○○にしたいとき、道幅は何mとれるか考える問題です。2次方程式を使って解決します。道の本数は縦横1本ずつから最大3本ずつまで選べます。条件設定が難しく、動かし方次第で道が重なってしまうので、重ならないように動かしてください。
2次方程式の利用〜動点〜
正方形の辺上の2点P,Qが同時に動くときにできる三角形の面積に関わる問題です。正方形の大きさを変えられます。
上の問題の点P,Qの位置が違う版です。グラフも表示できますが…
直角三角形の辺上の2点P,Qが同時に動くときにできる台形の面積に関わる問題です。直角三角形の大きさを変えられます。
関数の導入
正方形ARQPの一辺の長さに伴って変わる数量はどんなものがあるがろうか…
斜面を転がるボール
斜面を転がるボールです。角度や重力加速度など変更できるようにしてあります。教科書の例のように綺麗な式になることはほとんどないですね。理科が好きな生徒にとっても興味深いものだと思います。
斜面を滑る物体
摩擦・空気抵抗をなしとして,斜面を滑る物体は等加速度直線運動をします。斜面を滑り終わると等速直線運動をします。高校物理の話につなげられればと思ってつくりました。
変化の割合の意味
自由落下のときの平均の速度が変化の割合と等しいことを学習するときに使います。重力加速度を変えられます。
y=ax^2のグラフ

↓↑旧VB版(WinPCのみ可)
geogebraの良さとしてどこまでも拡大・縮小ができることです。曲線を点で描いた時,一見曲線に見えても,拡大すると確かに点の集まりで描かれていることが確認できます。
ともなって変化する値
ともなって変化する値ver.2
2乗に比例する関数において,xの値にともなって,yの値が変化する様子を示します。もちろん比例定数を変化させることもできますよ。
身近に現れる関数y=ax^2
よくある「定速で走るランナー」とある区間まで「加速して走る自転車」の関係から関数関係を見出す問題です。チェックを入れると自転車が現れたり,グラフが現れたりします。
身近に現れる関数y=ax^2(グラフなし版)
上記のグラフなし版です。H先生の依頼により作成。
重なった図形の面積
四角形に三角形がめりこんで?いきます。重なった部分の面積はどのように変化していくでしょうか。図形にともなってグラフを表示します。
ver.2です。少し見やすくなった…はず!
四角形の辺上を動く点①
四角形の辺上を動く点②
長方形や正方形の辺上を動く点があり,それらや頂点で結んでできる三角形の面積がどのように変化するかを示したものです。図形にともなってグラフを表示します。
5.相似
相似な図形

↓↑旧VB版(WinPCのみ可)
相似な図形のかき方
三角形と比の性質
平行線と線分の比
平行線と線分の比です。平行ということを維持したままいろいろと動かせます。
中点連結定理
中点によっ��てできる四角形
四角形の各辺の中点をつないでできる四角形はどんな四角形ができるだろうか?平行四辺形?ひし形?長方形?
相似な立体
倍率を操作して、相似な三角錐を表示することができます。
直方体versionもどうぞ
測量への利用
時間に合わせて太陽が動くので影が伸び縮みします。人の身長や、影の長さから測れない高いものの高さを求めてみましょう。太陽の動きは春分・秋分の日の北緯35°の太陽の動きにしてあります。
太陽の動き(神視点・人視点)
理科で学習する太陽の動きです。完全に理科の教材です。日本の場合しか扱わない場合が多いですが、すべての季節・すべての緯度での表示が可能です。
折り紙を折ってできる相似な三角形
まとめの問題にでてきそうな、長方形の紙を折ってできた三角形が相似が証明する問題です。まず、折り目がどこになるかをさがすところからですね。
正三角形の折り紙を折ってみる
正方形の折り紙だけでなく、正三角形の折り紙を折ってみたら何か関係のありそうな図形は見つかるかな?(埼玉県Iさんからのご依頼)
自然界にみられる黄金比
360°を黄金比に分割する角度分だけ、点を回転させます。そして、回転の中心から少しだけ遠くに点をとります。この��作業を繰り返すと、点はある植物に見えてきませんか?
円周角の定理
円周角の定理の発見?です。いつものようにぐりぐり動かしてみて下さい。角度を表示したり,補助線を表示したりすることができますよ。
円周角の定理[改]
上の「円周角の定理の発見」の改良版です。円周上の点P
を円外や円内に移動できるようにしたり,点Pの位置を3カ所まで保存できるようにしてあります。
円周角の定理の逆
円周角の定理の逆の発見です。2点A,Bを固定して,円周角にあたる角Pの大きさを維持したまま動かすことができます。角Pの大きさを変えられることがお気に入り。
円周角の定理を使った証明
円周角の定理の発展
円周角の定理の発展です。弧ABに対する円周角の∠APBと∠AQBがあるとき、円周上の点QをだんだんとBに近づていったとき、どんなことがいえそうですか。
三平方の定理の証明
三平方の定理の証明2
三平方の定理の証明3
授業では教科「書」であることから,動的に示す事は困難です。動的に示すことは,「いつでも成り立つ」ことを直感的に理解する上で大切だと個人的には思います。1~3のどれも中心の三角形ABCの頂点を移動させることができます。また3つ目はボタン1つで完全自動で見られます。
直方体の中を通る線分
直方体の対角線といったらよいのでしょうか。なかなかイメージしづらいですね。長さを求めるためにはいつものあれを見つければいいよ。Hintにチェックを入れましょう。
直方体の表面を通るひもの長さ
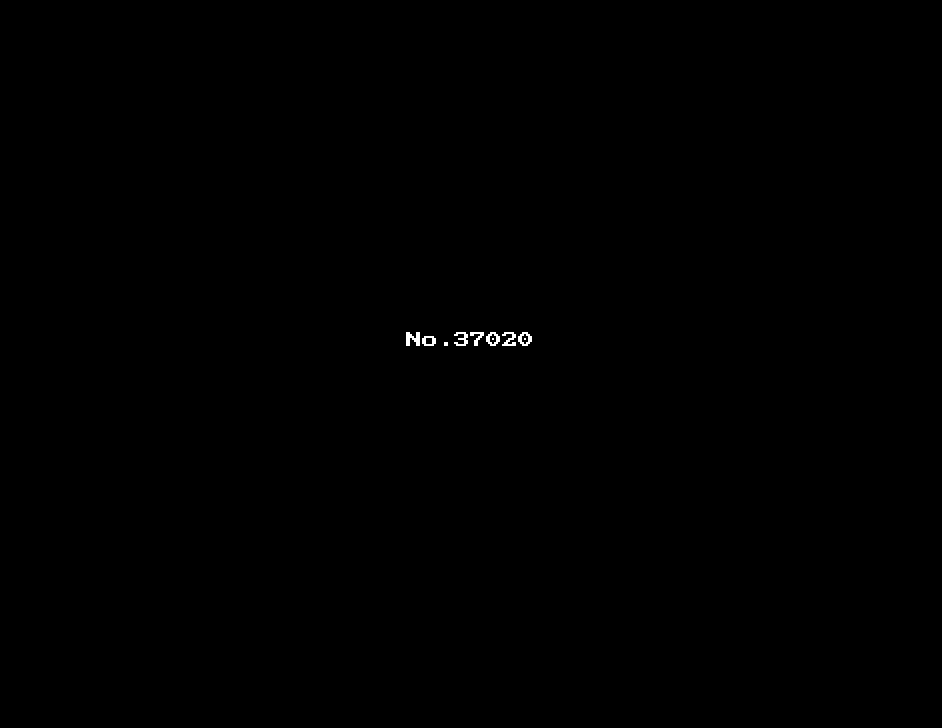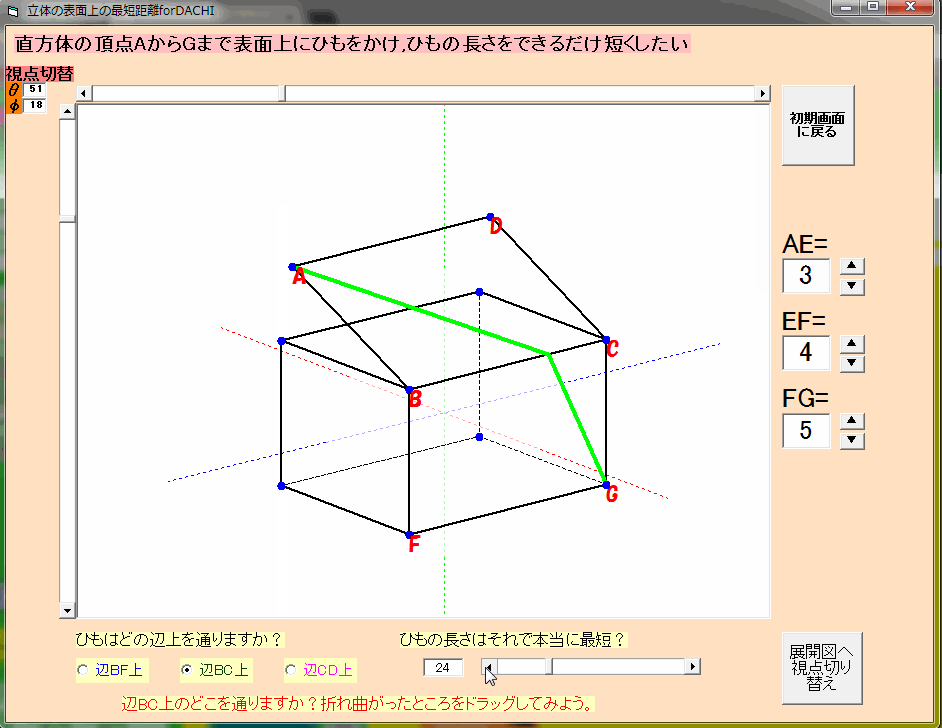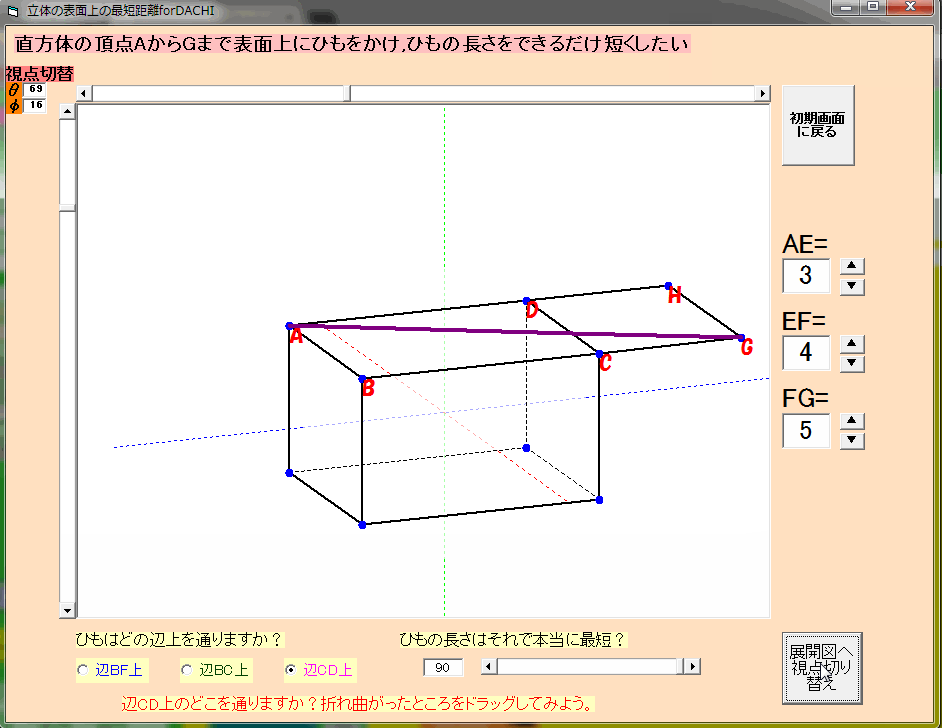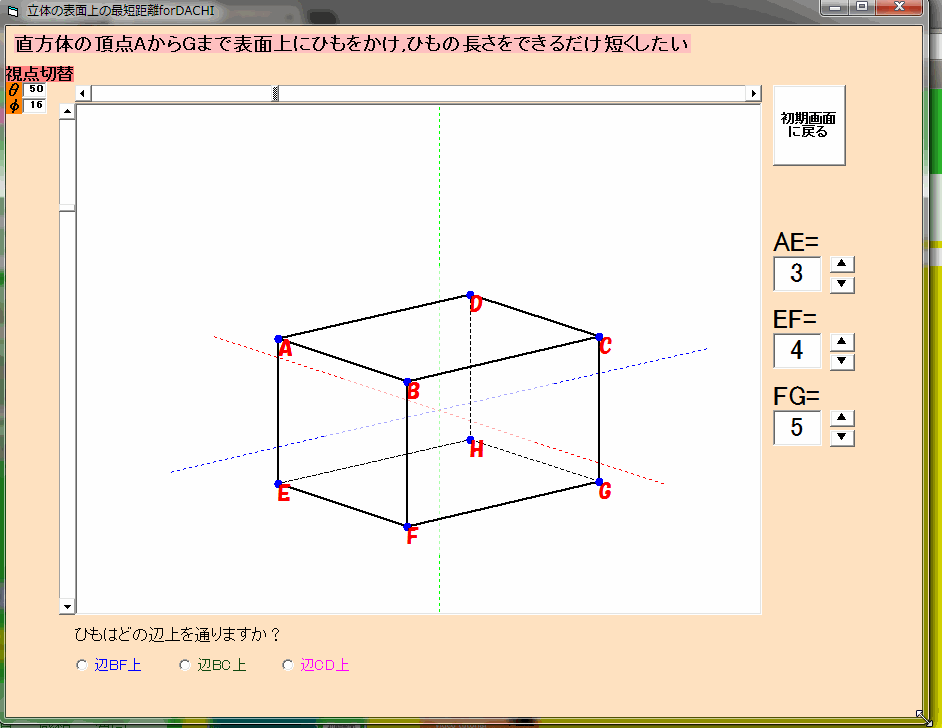
↓↑旧VB版(WinPCのみ可)
直方体の表面を通るひもの長さです。折れ曲がっているひもの最短の長さを考えるときに,見事に1年生の学習内容と繋がるのがおもしろい。以前VBで作っていたときはスカスカの直方体でしたが,GeoGebraでは見事に改善。

データの活用については正進社の「SGRAPA」(スグラパ)を用います。
https://sgrapa.com/
step1.まずこの下にある使いたいデータを
PC・タブレットに保存します。
・もとのデータを使用する場合は.csvを
・プロジェクトを使用する場合は.jsonを ダウンロードする。
※タブレットの場合は「ファイル」に保存しておく。
step2.スグラパのネット版を開き、
先ほどダウンロードしておいたファイルを開く
・もとのデータを使用する場合は.csvを
・プロジェクトを使用する場合は.jsonを 開く
sgrapa01_ハンドボール投げの結果【実データ】
sgrapa02_ハンドボール投げの結果【標本平均】

















































