2nd grade in junior high school
2年生は合同の証明や平行四辺形であることの証明など,論証をより深く学んでいきますね。合同条件を見つけるなどパズルをはめていくようで楽しかったです。
三角形の内角の和は180°であることなど,図形の形を変えてもいつでもいえることの理解を,これらの教材がサポートしてくれると嬉しいです。
2.連立方程式
7.確率
文字式の利用：陸上トラックのスタート地点
1.式と計算
陸上トラックのセパレートコースはスタート地点がずれています。スタート地点を同じにしては外側のコースの人が不利だからです。では，その差は何に影響されて決まるのか…コーナーの半径？ストレートの長さ？各コースの幅？
いろいろ操作して探ってみてください。
１次関数導入：お魚レース
3.1次関数
３匹の魚のレースの様子をグラフをもとに考えます。
うまく実況を考えましょう。チェックをいれると魚の
イラストを表示させることができます。
１次関数導入：紙を折るときにともなって変わる数量
長方形の紙を折ります。折った長さにともなって変化する数量にはどんなものがあるだろうか。いつも実物を渡すのですが,変化する様子を動的に見せるために創りました。
1次関数導入：配膳台を動かしたときに現れる関数
１次関数の導入の教材は、封筒、折り紙など机の上で実物をさわりながら考えられるものが多かったのですが、配膳台の登場です。教師が前で示しやすいから？時代に逆行？
1次関数のグラフ
1 次関数のグラフを表示します。直線を表示することもできれば，点をプロットさせることもできます。a,bの値を連続して変化できるようにもしてあります。
1次関数のグラフを最大３本表示させることができます。２本のグラフが平行になる条件や、垂直に交わる条件などを考えさせてもよいかもしれませんね。
２元１次方程式のグラフ
２元１次方程式のグラフを表示します。数は整数しか対応していまが、クリックで数字を大小させることができます。また座標平面の右上・左下の点を移動させれば、座標平面の表示範囲を変えることができます。スクショすれば、プリント作成するときに便利かと…
２元１次方程式のグラフ（３本）
２元１次方程式のグラフを同時に最大３本表示できます。グラフと連立方程式の学習や平行な２本・垂直な２本のグラフを表示させるときにご活用ください。
1次関数の利用
日常的な問題を１次関数のグラフを用いて解決します。Aさんは、図書館に行ってからBさんの家に向かいます。バスは駅と図書館を往復しています。それぞれ速さや休憩時間を変更できるようになっています。
四角形の辺上を動く点①
四角形の辺上を動く点②
四角形の辺上を動く点③
四角形の辺上を動く点④
図形の辺上を動く点がつくる三角形の面積の変化をとらえる問題いろいろ。もとの長方形や三角形の頂点を動かせば長さを変えられます。どれもスタートボタンを押せば点が動き出します。④は２つの動点です。
四角形の辺上を動く点④.5
上の問題のサイズが半分のバージョンです。（ただ点Aを動かしただけですが）
4.平行と合同
対頂角・同位角・錯角
始めは２直線が表示され対頂角の学習に使います。そしてボタンを押していくと,３本目が表示されたり，平行線にひけたりします。対頂角・同位角・錯角が単発でなく,つながりをもって理解してほしいと思い作りました。
三角形の内角の和
三角形の内角の和は，本当にいつも180°なのだろうか？補助線を引いて考えてみよう。いつものように点A,B,Cを移動させることができます。
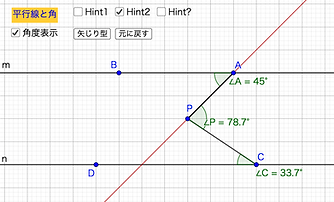
平行な２直線と角,矢じり型
よくある平行な２直線にくの字型に線分が引かれている教材です。くの字の頂点にあたる点Pを移動させたり,平行な２直線を移動し,矢じり型を作れるようになっています。これもつながりを意識して作りました。
↑はじめからm//nになっていない版
（ボタン１つで平行にできます。）
多角形の内角の和
五角形の外角の和
多角形の外角 の和
星型多角形の角の和(n/2)
星型多角形の角の和(n/3)
多角形の内角や外角の和を調べる教材です。頂点の移動はもちろん,13角形まで頂点の数を増やせます。星型多角形に関しては，１つとばしの頂点を結ぶn/2角形と２つとばしの頂点を結ぶn/3角形の２種類用意しました。
角の二等分線の作図と証明
スラーダーを操作して，順番に作図手順を表示します。もちろん半直線の開き具合は操作できますので，10°ほどの小さな角の二等分線から170°の角の二等分線もかけます。ただ180°を越えると…
証明の単元用に仮定・結論のチェックを入れると辺や角を表示します。
5.三角形と四角形
三角形の合同証明
よくみかける問題は△ABC,△CDEが正三角形のとき△ACD≡△BCEの証明。角度を変えて二等辺三角形にできたり，△ABCに対する△CDEの大きさを変えられるようにしてあります。
平行四辺形であることの証明
△ABCの各辺を一辺とする正三角形をかくと，四角形AFEDは平行四辺形になることの証明。発展問題です。点Aの位置によっては四角形AFEDが長方形になたり，ひし形になったりします。その成立条件を考えても面白い。
特別な平行四辺形をつくろう
点A,B,Cを自由に動かせます。四角形ABCDは常に平行四辺形になるように点Ｄは自動で動きます。四角形ABCDがひし形や正方形、長方形になったときに図形に色がつきます。どんな条件の時に特別な平行四辺形になるか探ってみましょう。
等積変形_三角形
等積変形_四角形
平行線による等積変形です。チェックを入れると高さが表示されるようになっています。これはK先生作成によるもの。専門的な知識も不要で作りやすいのがGeoGebraの特徴ですね。
等積変形_平行四辺形
平行四辺形内の面積の等しい三角形を見つける問題です。向きはさまざまですが多くの場合このような対角線や線分をひいた図形をよく目にします。
等積変形_土地の分割
等積変形_三角形の二等分
もとになったK先生が創った等積変形の教材を応用して創りました。こんなことが容易にでｋるのもGeogebraの良さです。
平行四辺形の性質の利用
平行四辺形の性質を利用して、遊園地の「空飛ぶじゅうたん」はなぜ地面と平行かを考える教材。sin曲線を利用して動きを表現することが上手くできたと思います。
生活の中の平行四辺形
我が家にある裁縫道具入れです。平行四辺形であるための条件を見事に利用した道具だと思います。
折り返してできる図形
ある帯を折り返して重なった部分が◯◯◯三角形になっていて、それはなぜかを考える問題をよく見かけます。その帯を正方形にしたり、平行四辺形に変えらるようにしてあります。またいろいろな方向に折り曲げられます。
6.データ比較と箱ひげ図
データの活用については正進社の「SGRAPA」(スグラパ)を用います。
https://sgrapa.com/
step1.まずこの下にある使いたいデータを
PC・タブレットに保存します。
・もとのデータを使用する場合は.csvを
・プロジェクトを使用する場合は.jsonを ダウンロードする。
※タブレットの場合は「ファイル」に保存しておく。
step2.スグラパのネット版を開き、
先ほどダウンロードしておいたファイルを開く
・もとのデータを使用する場合は.csvを
・プロジェクトを使用する場合は.jsonを 開く
sgrapa01_1月の各日の平均気温
